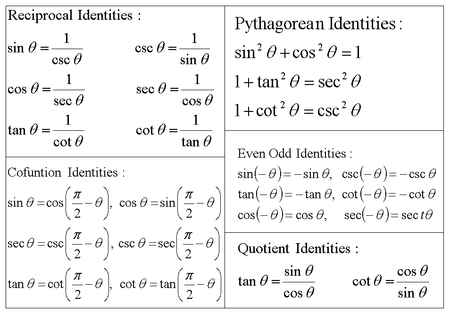
Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosine1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θTrigonometric Identities prove tan^2 (x)sin^2 (x)=tan^2 (x)sin^2 (x)

Worksheet On Trigonometric Identities Establishing Identities Hints
Trig identities tan^2
Trig identities tan^2-Now, using the trigonometric identity 1tan 2 a = sec 2 a sec 2 A = 1 (3/4) 2 sec 2 A = 25/16 sec A = ±5/4 Since, the ratio of lengths is positive, we can neglect sec A = 5/4 Therefore, sec A = 5/4 Example 2 (1 – sin A)/(1 sin A) = (sec A – tan A) 2 Solution Let us take the Left hand side of the equation LHS = (1 – sin A)/(1 sin A)Trigonometric Identities MTH 151 Reciprocal Identities csct= 1 sint (1) sint= 1 csct (2) sect= 1 cost (3) cost= 1 sect (4) cott= 1 tant (5) tant= 1 cott (6) Tangent and Cotangent tant= sint cost (7) cott= cost sint (8) Pythagorean Identities sin2 tcos2 t= 1 (9) 1cot2 t= csc2 t (10) tan2 t1 = sec2 t (11) Formulas for Negatives sin( t) = sint
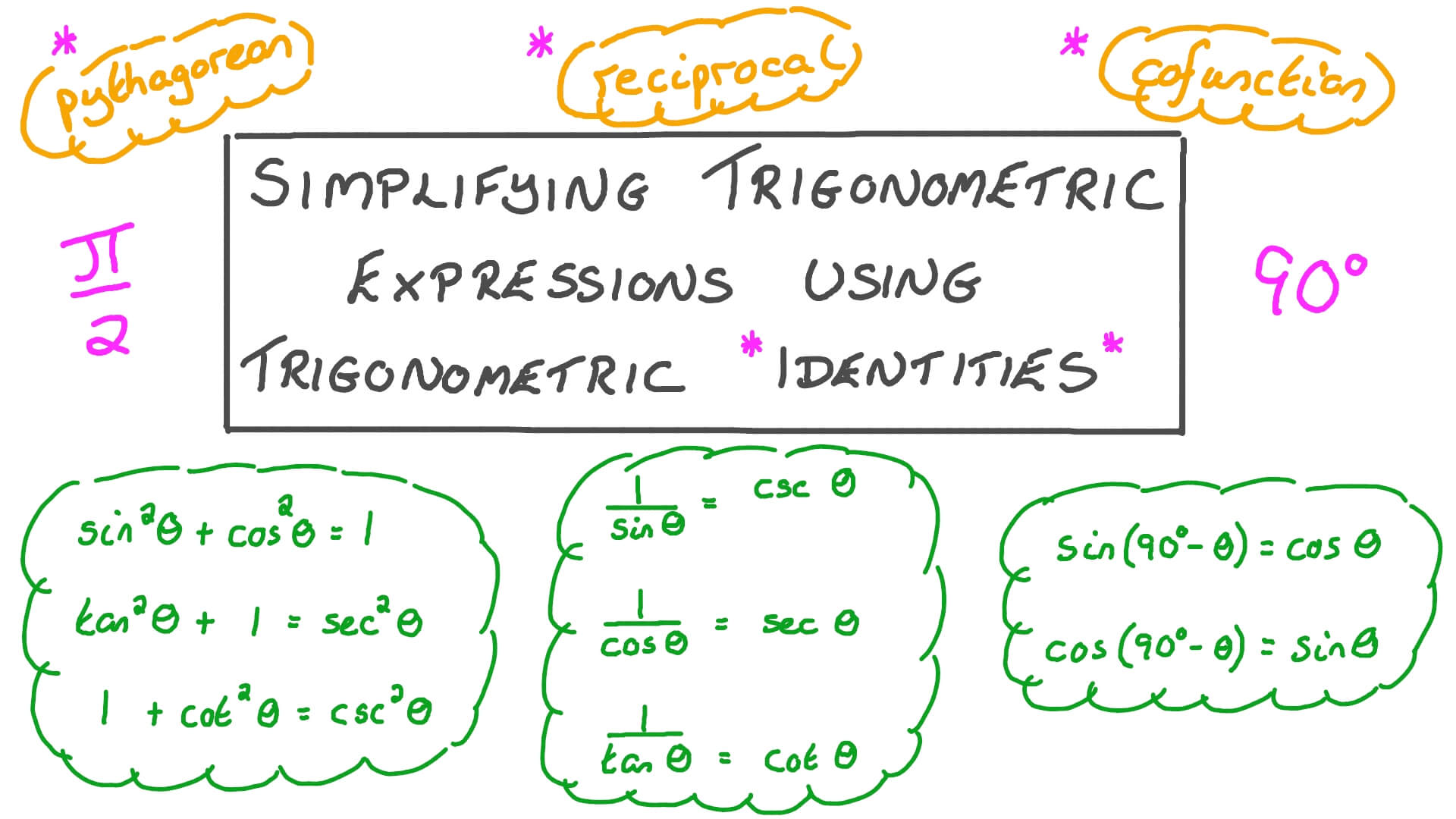



Lesson Video Simplifying Trigonometric Expressions Using Trigonometric Identities Nagwa
Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2Derivatives of Trigonometric Functions The basic trigonometric functions include the following 6 functions sine (sinx), cosine (cosx), tangent (tanx), cotangent (cotx), secant (secx) and cosecant (cscx) All these functions are continuous and differentiable in their domainsA Trigonometric identity is an identity that contains the trigonometric functions sin, cos, tan, cot, sec or csc Trigonometric identities can be used to Simplify trigonometric expressions Solve trigonometric equations Prove that one trigonometric expression is equivalent to another, so that we can replace the first expression by the second
Tan is an "odd" identity quotient identity (for tangent) algebra/ simplify 1) 2) cos tan (x) Strategy 1) get rid of the negatives 2) üy to change terms to sin's and COS's 3) simplFy • tan (x) tan x sm x cos x smx cos (x) cosx • cosx • Prove StrategyProve tan^2 (x)sin^2 (x)=tan^2 (x)sin^2 (x) Trigonometric Identities Solver Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to SumIdentities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11
Prove the identity \(~~1 \tan^2 t = \dfrac{1}{\cos^2 t}\) Solution By manipulating the left side of the equation, we will show that the expression \(1 \tan^2 t\)For any value of \(x\), this equation is true Trig identities are sort of like puzzles since you have toAll the trigonometric identities on one page Color coded Mobile friendly With PDF and JPG downloads Trig Identities Download PDF Download JPG Reciprocal Identities I highly recommend this 3minute $$ \tan(2\theta) = \frac{2\tan\theta}{1\tan^2\theta} $$




Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities



Summary Of Trigonometric Identities
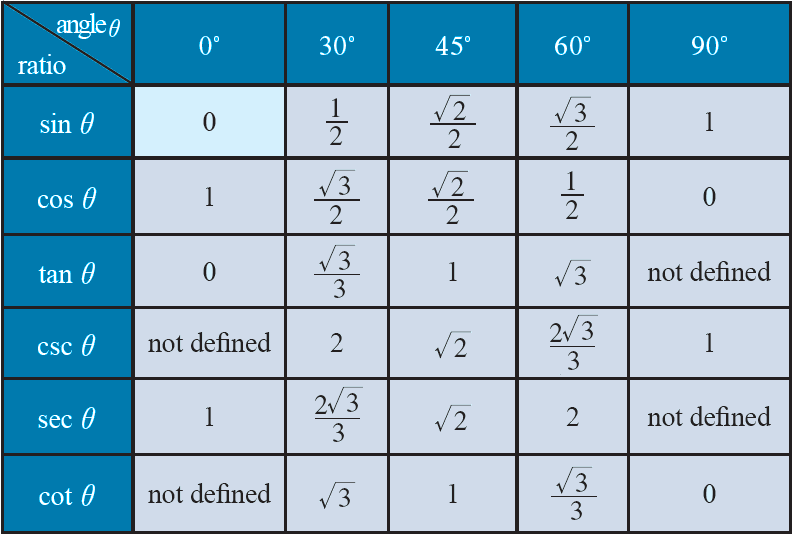
Trig Equations and Identities wwwnaikermathscom 4 (a) Given that sin q = 5 cos q, find the value of tan q (1) (b) Hence, or otherwise, find the values of q in the interval 0 £ q < 360° for which sin q = 5 cos q, giving your answers to 1 decimal place (3) June 06 Q6 5 (a) Show that the equation 3 sin2 q – 2 cos2 q = 1 can be written asSin 2 (x) cos 2 (x) = 1 tan 2 (x) 1 = sec 2 (x) cot 2 (x) 1 = csc 2 (x) sin(x y) = sin x cos y cos x sin y cos(x y) = cos x cosy sin x sin yTan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) cos x cos y = 2 sin ( (x y)/2 ) sin ( (x y)/2 ) Trig Table of Common Angles angle
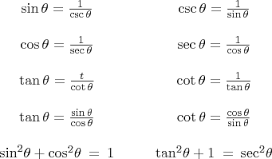



Math Review Of Trigonometric Identities Free Homework Help
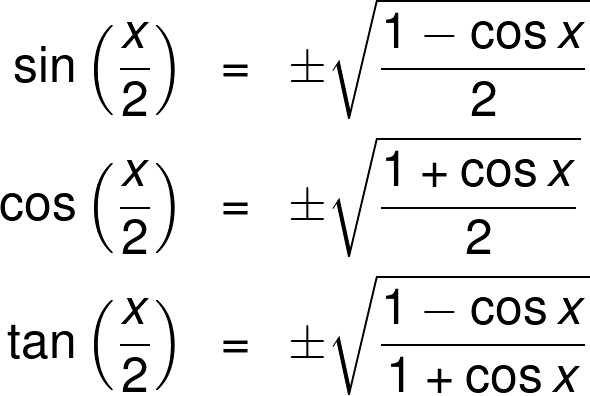



Half Angle Calculator
Trig identities tan^2Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos CompoundThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tanVerifying trigonometric identities can be super fun!Tan²θ = sin²θ cos²θ = 1 That is wrong tan²θ = sin²θ/cos²θ Secondly, the identity is tan²θ 1 = sec²θ, not tan²θ 1 Maybe this proof will be easier to follow tan²θ 1 = sin²θ/cos²θ 1 = sin²θ/cos²θ cos²θ/cos²θ = (sin²θ cos²θ)/cos²θ //sin²θ cos²θ =




Trigonometric Identities A Plus Topper



2
Trig Cheat Sheet Definition of the Trig Functions Right triangle definition For this definition we assume that 0 2 pLHS = 1 sin θ cos θ = ( 1 sin θ) cos θ) × ( 1 − sin θ) 1 − sin θ = 1 − sin 2 θ cos θ ( 1 − sin θ) = cos 2 θ cos θ ( 1 − sin θ) = cos θ ( 1 − sin θ) = RHS Restrictions undefined where cos θ = 0, sin θ = 1 and where tan θ is undefined Therefore θ ≠ 90 °; Simplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 1




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



Derivatives Of Trigonometric Functions Web Formulas
The key Pythagorean Trigonometric identity is sin2(t) cos2(t) = 1 tan2(t) 1 = sec2(t) 1 cot2(t) = csc2(t)Trigonometry Identities Examples and Strategies cosine is an "even" identity;Trigonometric Identities 43 Introduction A trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles) There are a very large number of such identities In this Section we discuss only the most important and widely used Any engineer using trigonometry in an application




Integrate Sec 2x Method 1




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions
Using the following tan(x) = sin(x)/cos(x) cos^2(x)sin^2(x) = 1 sec(x) = 1/cos(x) for cos(x)!=0, we have 1tan^2(x) = cos^2(x)/cos^2(x) (sin(x)/cos(x))^2 =cos^2(x)/cos^2(x)sin^2(x)/cos^2(x) =(cos^2(x)sin^2(x))/cos^2(x) =1/cos^2(x)Like looking in a mirror An example of a trig identity is \(\displaystyle \csc (x)=\frac{1}{\sin (x)}\);The key Pythagorean Trigonometric identity are sin2(t) cos2(t) = 1 tan2(t) 1 = sec2(t) 1 cot2(t) = csc2(t)




Trigonometric Identities 1 Conditional Trigonometrical Identities We Have Certain Trigonometric Iden Trigonometric Identities Trig Identities Maths Solutions




Solved 1 Using Various Trig Identities Determine The Ex Chegg Com
Pythagorean identities cos 2 (θ) sin 2 (θ) = 1 1 tan 2 (θ) = sec 2 (θ) 1 cot 2 (θ) = csc 2 (θ) Example Verify that cos (x)·tan (x) csc (x)·cos 2 (x) = csc (x) using trigonometric identities cos (x)·tan (x) csc (x)·cos 2 (x) = =TRIGONOMETRIC IDENTITIES A N IDENTITY IS AN EQUALITY that is true for any value of the variable (An equation is an equality that is true only for certain values of the variable) In algebra, for example, we have this identity ( x 5) ( x − 5) = x2 − 25270 ° Show Answer



7 Proving Ids Trig Functions Identities




Simplify Each Of The Following Trigonometric Chegg Com
And also very frustrating when you can't figure them out It can be tricky because there's no precise waTRIGONOMETRIC IDENTITIES By Joanna GuttLehr, Pinnacle Learning Lab, last updated 5/08 Pythagorean Identities sin (A) cos (A) 1 1 tan (A) sec (A) 1 cot (A) csc2 (A)Quotient Identities sin( )Section 72 Verifying Trig Identities Day 1 Dec 1801 AM 72 Verifying Trigonometric Identities *Transform one side of the equation until it is the same as the other side *Changing only one sides eliminates many possible errors Verify 1 1 tan2θ = sec2θ 1 sin2θ 2 cosθ cos 2θ sinθ cos2θ cos2θ cos2θ sin2θ




Trigonometric Identities




Revision Trigonometry Siyavula
The first equation below is the most important one to know, and you'll see it often when using trig identities $$sin^2(θ) cos^2(θ) = 1$$ $$tan^2(θ) 1 = sec^2(θ)$$ $$1 cot^2(θ) = csc^2(θ)$$ Cofunction Identities Each of the trig functions equals its cofunction evaluated at the complementary angle $$sin(θ) = cos({π/2} θ)$$Trigonometry Identities Quotient Identities tan𝜃=sin𝜃 cos𝜃 cot𝜃=cos𝜃 sin𝜃 Reciprocal Identities csc𝜃= 1 sin𝜃 sec𝜃= 1 cos𝜃 cot𝜃= 1 tan𝜃 Pythagorean Identities sin2𝜃cos2𝜃=1 tan 2𝜃1=sec2𝜃 1cot2𝜃=csc2𝜃 Sum & Difference Identities sin( )=sin cos cos sinAnswers to Worksheet Review Trig Identities (basic) (ID 1) 1) tan2x sec2x cosx Use tan2x 1 = sec2x1 cosx Use secx = 1 cosxsecx 2) tanx secxDecompose into sine and cosine sinx cosx 1 cosx Simplify 1 sinx cosx 3) secx sin3x Use cscx = 1 sinx csc3xsecxUse secx = 1 cosx csc3x cosx 4) cosx secxDecompose into sine and cosine cosx 1



What Are The Quotient Identities For A Trigonometric Functions Socratic




We Wish To Prove The Following Trig Identity Tan X Chegg Com
The half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α)Trigonometric identities are equations that relate different trigonometric functions and are true for any value of the variable that is there in the domain Basically, an identity is an equation that holds true for all the values of the variable(s) present in it (sin θcosec θ) 2 (cos θsec θ) 2 =7tan 2 θcot 2Recall A trigonometric identity is an equation formed by the equivalence of two trigonometric expressions The solution to the equation must be the set of all values of the variable, in which both expressions are defined Examples Example 1 Consider the trigonometric equation




Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec




Trig Identities All List Of Trigonometric Identities Learn Trigonometry
The eight basic trigonometric identitiesare listed in Table 1 As we will see, they are all derived from the definition of the trigonometric functions Since many of the trigonometric identities have more than one form, we list the basic identity first and then give the most common equivalent forms 796 111 Introduction to Identities TABLE 1Answer (b) 1 Explanation The question is in the form of (a b) 2 (a b) 2 = a 2 b 2 2ab So, on applying the identity, and after expanding the given equation, we will get => cosec 2 A sin 2 A 2 cosec A sin A sec 2 A cos 2 A 2 sec A cos A cot 2 A tan 2 A 2 cot A tan A After solving it with using trigonometric identities, we will getAn "identity" is something that is always true, so you are typically either substituting or trying to get two sides of an equation to equal each otherThink of it as a reflection;



1




Trigonometric Identities Docsity



Gradea S Trigonometric Identities List




Lesson Video Simplifying Trigonometric Expressions Using Trigonometric Identities Nagwa




14 2 Trigonometric Identities




Tangent Identities
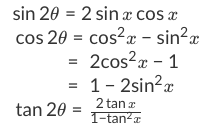



How To Use Double Angle Identities Studypug




Worksheet On Trigonometric Identities Establishing Identities Hints
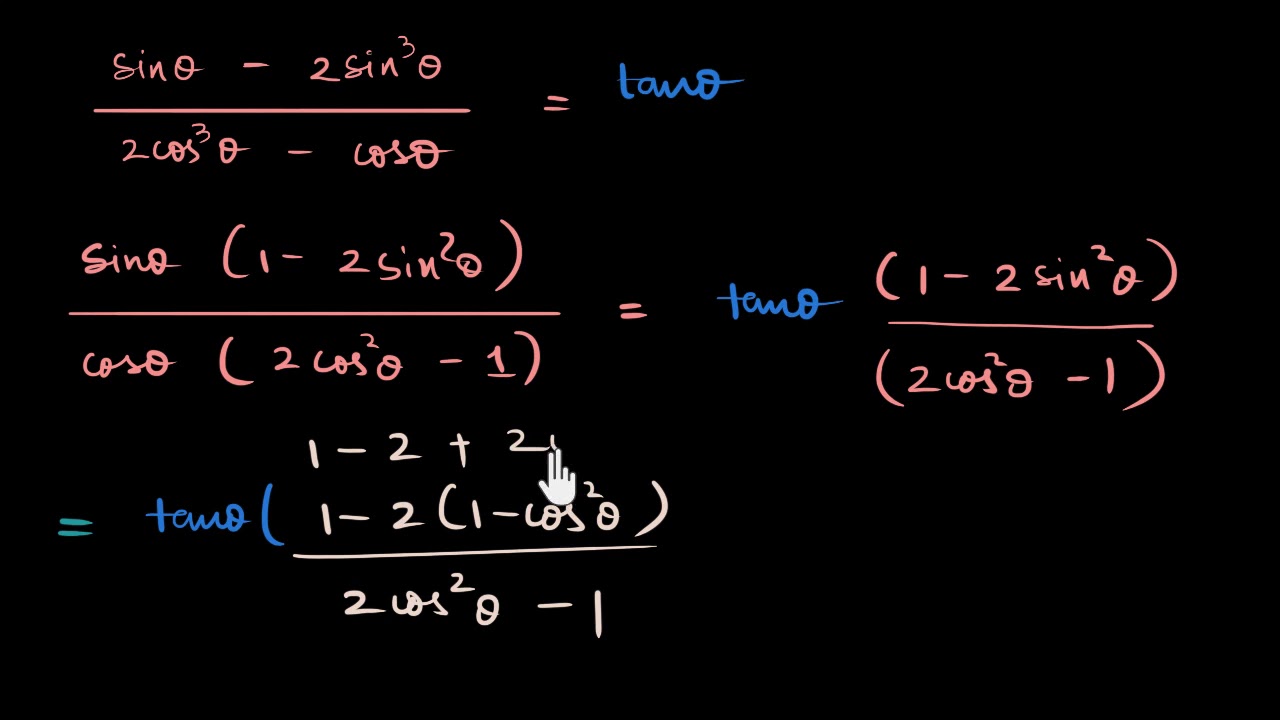



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy
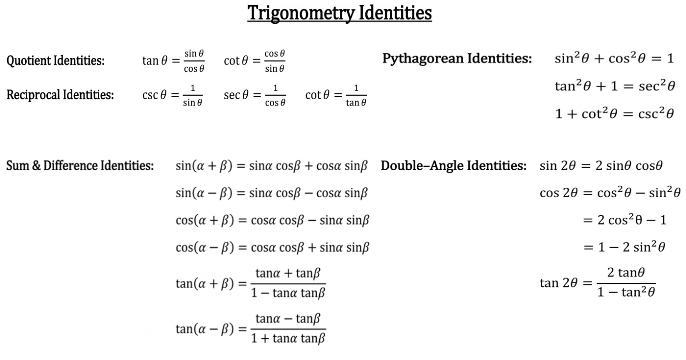



How To Prove Quotient And Reciprocal Identities Studypug




Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic




Trig Identities For Pre Calculus Dummies
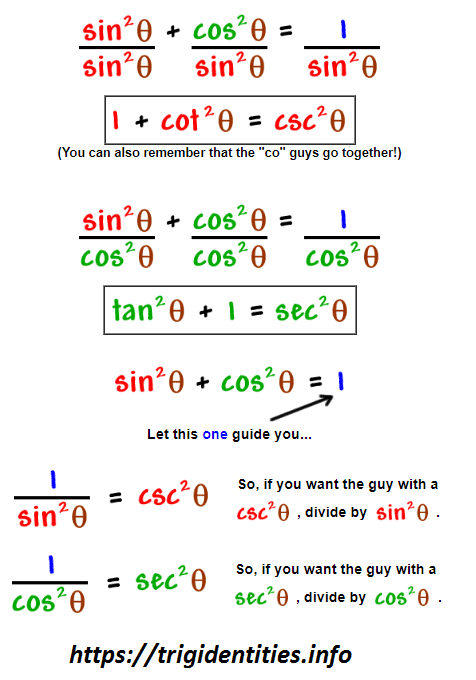



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities



1
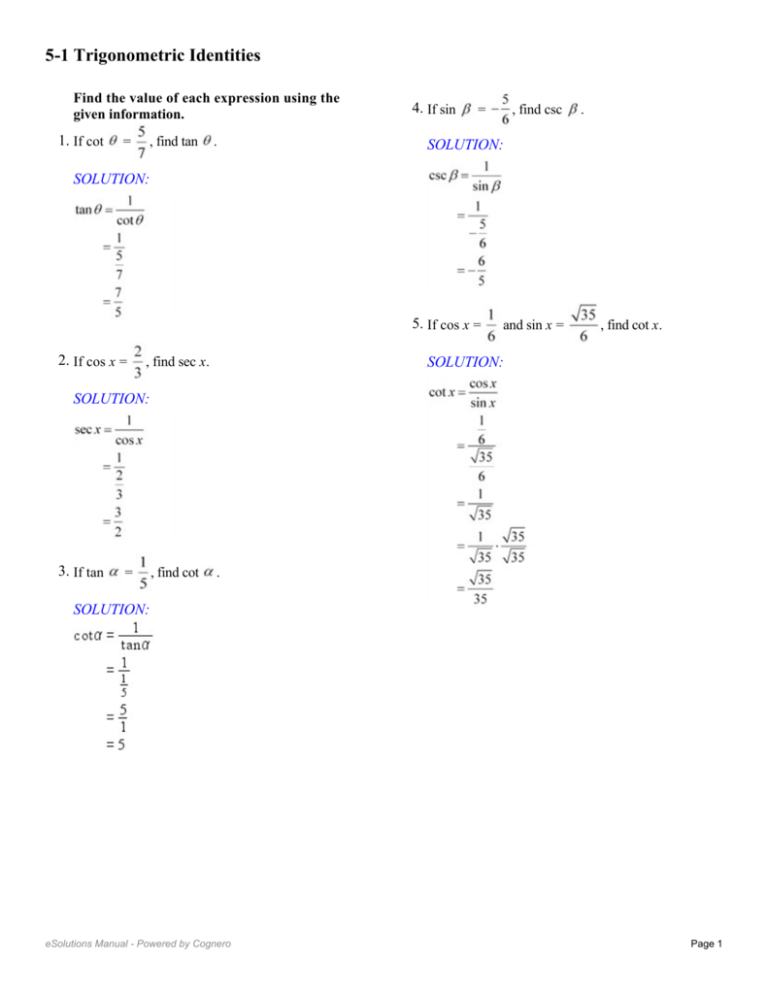



5 1 Trigonometric Identities



What Does It Mean To Prove A Trigonometric Identity Socratic




Powers Of Trigonometric Functions




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




14 2 Trigonometric Identities



Lesson 5 1 Trigonometric Identities Fiveminute Check Over




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions



The Trigonometric Ratios Of Angl



1




Integrate Sec 2x Method 2




List Of Trigonometric Identities Wikipedia




10 1 Reciprocal And Pythagorean Identities Mathematics Libretexts




Summary Of Trigonometric Identities




Reciprocal Identities In Trigonometry With Examples Owlcation




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Proving Trigonometric Identities



6 1 2 Trigonometric Identities



A Trig Identity



How I Remember Trig Identities Part 2 Beyond Solutions




We Wish To Prove The Following Trig Identity Cos 2 Chegg Com




Trigonometric Identities Solutions Examples Videos




List Of Trigonometric Identities Wikipedia




Summary Of Trigonometric Identities



1




Summary Of Trigonometric Identities



Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig
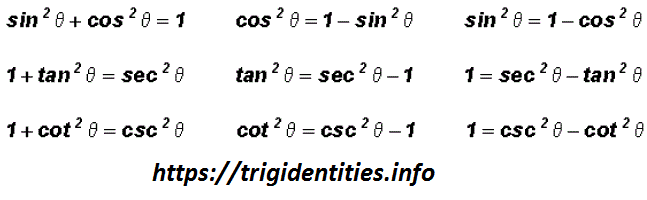



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities




Chapter 5 Trigonometric Identities Review Sheet




Tangent Identities




Trigonometric Identities Proofs List Of All Trig Identities
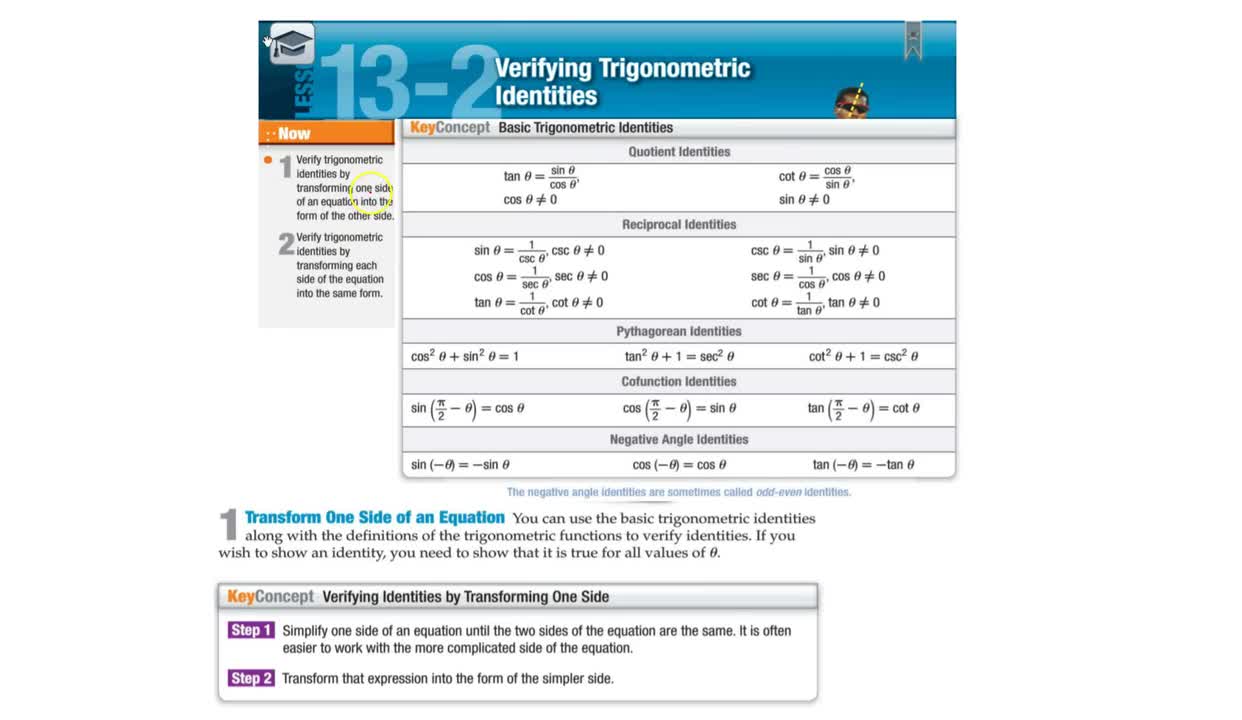



Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School




Trigonometric Identities List Of Trigonometric Identities Examples




Trig Identities Bingo Card




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X 1 Ppt Powerpoint




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube



Derivatives Of Trigonometric Functions
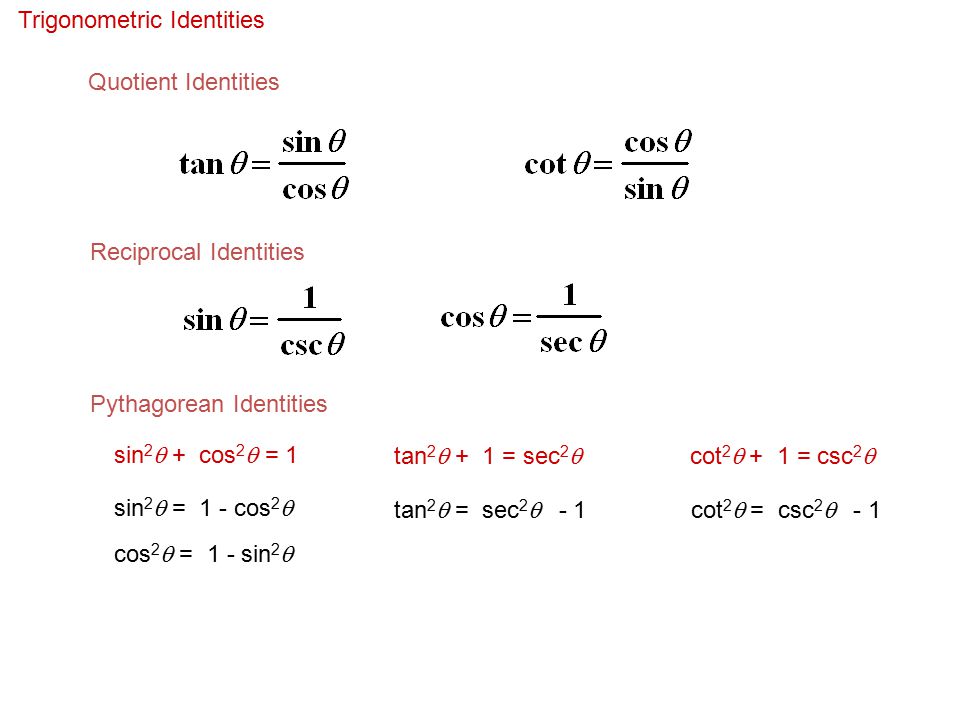



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download




Analytic Trig Ppt Video Online Download



What Is The Formula Of Tan2x Quora




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




2sinxcosx Trig Identity Gamers Smart




Trigonometric Identity 1 Sin X 1 Sin X Sec X Tan X 2 Cbse 10 Youtube




Tangent Half Angle Formula Wikipedia



2




Pre Calculus Section 7




2 Prove The Following Trig Identities A Prove Tan Chegg Com
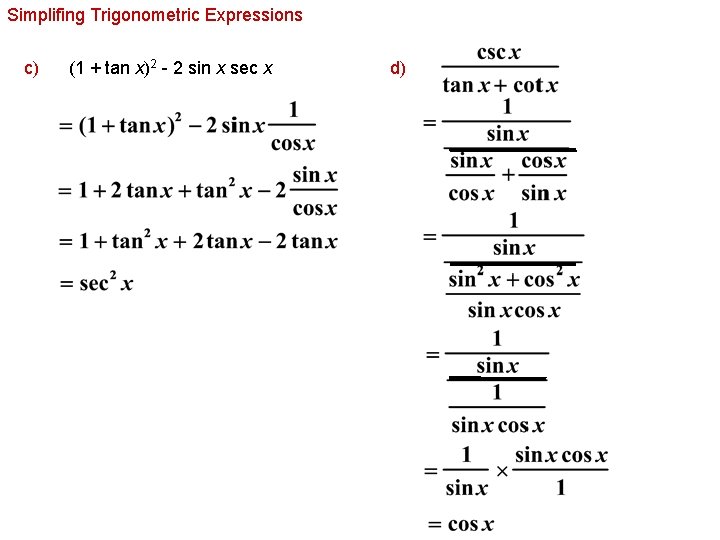



While You Wait Trigonometric Identities And Equations Section




14 2 Trigonometric Identities




Tangent Half Angle Formula Wikipedia




Verifying Trigonometric Identities Process Make One Side Look




Trigonometric Identities Topics In Trigonometry



Trig Identities Bingo Card
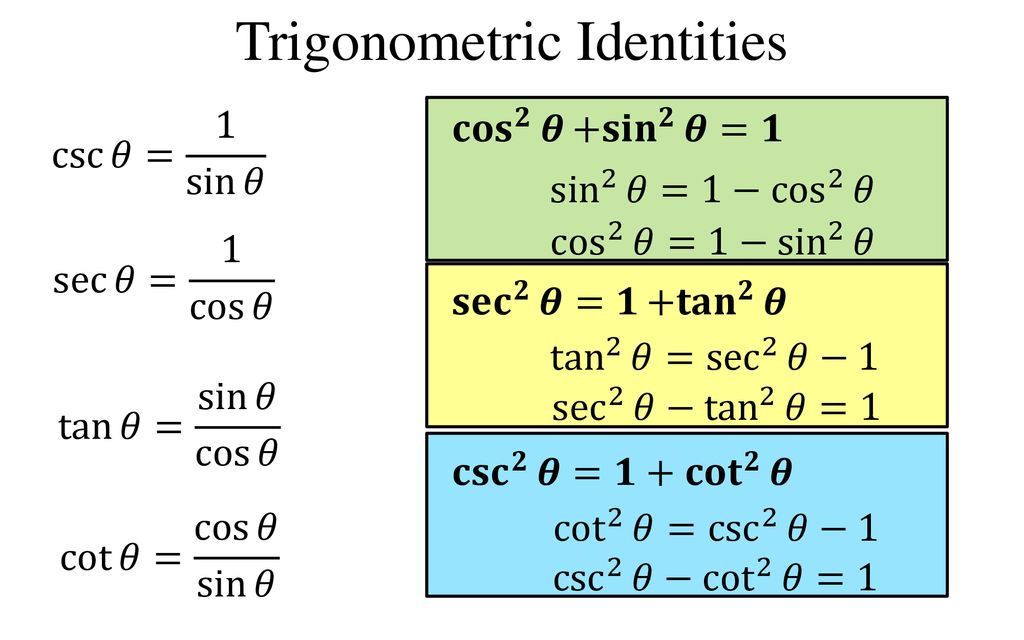



Trigonometric Identities And Equations Ppt Download



Solved Find The Remaining Five Trigonometric Functions Of 0 See Example 1 Sin A 0 In Quadrant Ii 32 Cos 0 0 In Quadrant I 33 Tan 0 Course Hero



5 1 Lesson On Trig Identities Schooltube Safe Video Sharing And Management For K12




Verify The Trigonometric Identity 1 1 Sin 2 X 1 Tan 2 X Youtube
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




5 2 Verifying Trigonometric Identities Copyright Cengage Learning
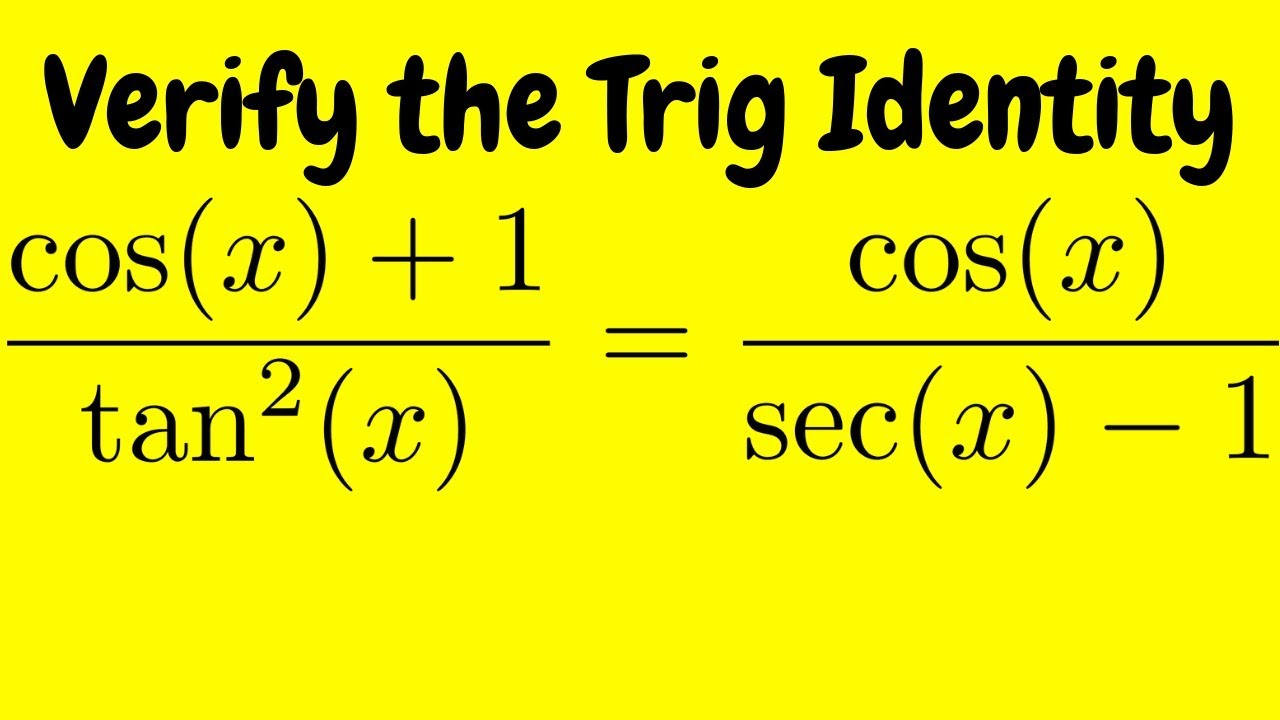



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube




Trig Identities Maple Learn Maplesoft
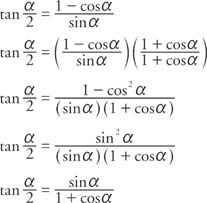



Tangent Identities



Trigonometric Identities




Chapter 11 Trigonometric Identities And Equations 11 1




Summary Of Trigonometric Identities



0 件のコメント:
コメントを投稿